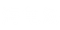答案与谜底【持续更新】
前几年的时候,因为偶然间看到了一些非常经典的趣味智力题,开始对于这类有趣的迷题产生了兴趣。幸运的是,我遇到了一些志同道合的伙伴,大家在共同解题的同时,一同也创造了许多有意思的迷题。这里所说的智力迷题,是指那些不需要具备一定相关知识和学术概念,仅凭借逻辑与常识并加以思考即可解决的趣味问题。我把那些问题都记录在了知乎的专栏内,并且将设计题目时的一些思考写了下来。这些迷题有些是来自于纯粹的灵感,而有些则是对于经典的改编。
直到最近,经常有人向我问起一些老题的解法。我这才发现我似乎拥有一个非常差的记忆力。我总是因为忘记解答过程而重新又自己做了一遍,然后在解题的过程中,总是会发现一些以前没有注意过的东西,有的是一个以往没有注意到的错误,而有的则是一个新的灵感。于是,我决定把所有问题的解法都记录下来,便于以后可以随时回顾与检查。
说明:
1.这篇解答文章会随着新题的出现而不断更新。
2.并非所有迷题都是有最终解的。我会把我自己的最优解列出来,如果您有找到比我更优的解法,请务必联系并告知我。
3.拓展部分的解答不会给出。(因为多半也给不出==!)
4.有任何想法想要与我交流的,永远欢迎。我的qq是:2764337159。
5.题图绘师:KoNE(pixiv id=28592204) 本作品pixiv id=66737136
那么开始吧!~
一.囚犯游戏

这个问题最朴素的想法就是归纳与逆推。事实上,很多迷题都可以通过类似的方法来打开思路。
首先考虑只有2个人的情况。假设为a,b,初始数字分别为1和2。在这种情况下2个人都没有别的选择,a必须与b的2换,然后b又把2换回来。结果:初始数字为1的a获得最终胜利,初始数字为2的b被淘汰。
然后考虑3人时的情况。假设为abc,初始数字分别为123。基于2人局的结果,本轮结束时拿到数字1的人将取得最终胜利。因为3是淘汰数字,a一旦拥有3,b和c不可能再来换a的3,所以a必然与b的2进行交换。同理,b也不会去换3,于是又与a换,把自己的2换回来。最后,c再与a交换得到1。结果:初始数字为3的c获得最终胜利,初始数字为1的a被淘汰。
再考虑4人时的情况。假设为abcd,初始数字1234。从3人局的结果来看,本轮拿到3的人将取得最终胜利。4是淘汰数字,所以a必然只与b或c换。这时我们考虑到一个问题,显然直到d开始换之前,没有人会去与d的4进行交换,于是d是必然可以换到数字3的。因此,对于abc而言,在d行动时,持有数字3就意味着被淘汰。因此,a与b都不会去换c的3。那么显然的结果就是a与b再次互换后,c选择与b的2进行交换(因为在3人局中,1是会被淘汰的初始数字)。最后,c与b的3进行交换。结果:初始数字为4的d获得最终胜利,初始数字为2的b被淘汰。
将4人局的结果带入5人局之中,再结合之前的分析方法,很容易得到在没有牺牲行为时,正常的结果:e拿到必胜数字4,d拿到次优数字3,a拿到5被淘汰。
综合以上过程,正常的淘汰顺序是ABCDE,E获得最终胜利。然而,结果却是DBCEA。其实观察逆序情况,很容易发现有猫腻的2个人就是A和D。那么该如何分析呢?从D的角度来看,D会第一个被淘汰只有2种可能。第一,D自己主动用自己的4去换了E的数字5,逼迫E不得不与A的3进行交换。第二,E放弃去换必胜的数字4,而去与D的次优数字3进行交换。可是在第二种情况中,E事实上只是从第5个淘汰降为了第4个淘汰。与题设"失去了不止一次的减刑机会"不符。因此,最终的结论只有一个:D牺牲了自己,帮助了A。
二.石头剪刀布

这个问题在最初设计的时候我并没有花费太多时间,然而过了很久之后的一天,有人突然问起我这个问题的解法时,我却因为忘记最初自己的解法,而花费了几乎比出题更长的时间才把它解开....或许我应该重新评估这个问题的难度。
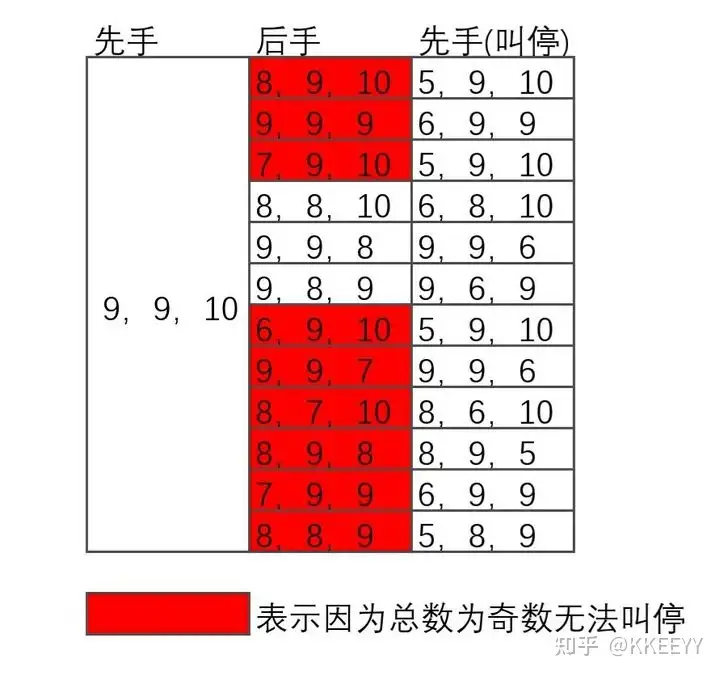
首先从简单的情况开始考虑。如果现在桌上只有两种卡片,那么很显然叫停并分叠的玩家是可以必胜的。假设两种卡片的数量分别为x和y,那么显然先手玩家必然可以胜MIN{x,y}MIN\left\{ x,y \right\}次(指x和y中的较小值)。那么通过加入第三种卡片,必然会开始影响叫停玩家的胜利次数,那么究竟加入多少时会导致胜的次数少于负的次数呢?由于三种卡片循环克制,我们不妨设剪刀(x张)和石头(y张)为较多的卡片,布(z张)从0开始增加。那么,两个叠堆的卡片数各为x+y+z2\frac{x+y+z}{2}张。根据鸽巢原理,无论后手如何安排一一对应, 先手叫停的玩家必然可以通过将x与y完全分置于两叠卡片中(假设没有一种卡片数大于总数的1/2),再选择其中一个叠堆来取得恰好x+y−x+y+z2=x+y−z2x+y-\frac{x+y+z}{2}=\frac{x+y-z}{2}次的胜利,而会输的局数恰好为zz局(始终假设z≤x,yz\leq x,y)。例如下图情况:

上图的例子当中, 在石头和剪刀分别有8张和7张的情况下,先手玩家必然可以通过选择左边的堆叠来获得5局必胜。
另外,对于存在某种卡片数量大于总数1/2的情况,结论也是显然的,叫停玩家可以将其中一叠全部分为同一种卡牌,然后叠堆2选1,后手玩家无任何可操作空间。
因此,我们可以得到一个叫停玩家必胜的充分条件:x+y−z2≥z\frac{x+y-z}{2}\geq z,
整理即得:z≤x+y+z4z\leq \frac{x+y+z}{4}。
接下来证明这个条件也是必要的。我们已经知道,仅考虑2种数量分别为x和y的卡片时,最多只能胜MIN{x,y}MIN\left\{ x,y \right\}局。对于后手玩家而言,面对两叠已经分好的牌叠,在决定一一对应顺序时,可以将局部的两种克制卡牌分在一起。
记后手玩家能取得的胜利局数为WW,其中能通过剪刀获得胜利的局数为WxWx,能通过石头获胜的局数为WyWy,能通过布获胜的局数为WzWz。则有
W=Wx+Wy+WzW=Wx+Wy+Wz
再令两名玩家的剪刀石头布卡片数量分别为Ax,Ay,Az,Bx,By,BzAx,Ay,Az,Bx,By,Bz。则有:
Wx=MIN{Ax,Bz}Wx=MIN\left\{A x,Bz \right\}
Wy=MIN{Ay,Bx}Wy=MIN\left\{A y,Bx \right\}
Wz=MIN{Az,By}Wz=MIN\left\{A z,By \right\}
当Ax=Bz,Ay=Bx,Az=ByAx=Bz,Ay=Bx,Az=By时,有
W=Wx+Wy+Wz=W=Wx+Wy+Wz=x+y+z2\frac{x+y+z}{2}≥\geqMIN{x,y,z}MIN\left\{ x,y,z \right\}。
除此之外,不妨设Bx,AzAx≥Bz,Ay>Bx,Az<ByAx \geq Bz,Ay>Bx,Az
W=Wx+Wy+Wz=Bz+Bx+Az=Bx+z≥z≥MIN{x,y,z}W=Wx+Wy+Wz=Bz+Bx+Az=Bx+z\geq z \geq MIN\left\{ x,y,z \right\}。
结论:无论叫停玩家如何分叠,后手玩家总能找到一种一一对应的方式,使得自己的胜利局数不少于数量最少的种类的卡片数。
不妨假设z≤y≤xz\leq y\leq x。当\frac{x+y+z}{4}">z>x+y+z4z> \frac{x+y+z}{4}时,记此时叫停的先手玩家的获胜局数为VV,则必有
V≤x+y+z2−W<x+y+z2−x+y+z4=x+y+z4<z≤WV\leq\frac{x+y+z}{2}-W<\frac{x+y+z}{2}-\frac{x+y+z}{4}=\frac{x+y+z}{4}
因此,z≤x+y+z4z\leq \frac{x+y+z}{4}是先手玩家必胜的必要条件。
最终的结论:当且仅当某种卡片的数量不超过所有卡片总数的4分之1时,此时叫停的玩家必定可以找到一种必胜的分叠方法。
接下来的工作就是枚举了。从先手开局的各种方式中,我们会发现(9,9,10)这种局面可以确保先手玩家的胜利。具体对应策略如下:
三.接错的灯泡

如果直接去枚举每次断电时的开关状态,或者尝试从这个角度去思考方案的话,其工作量是无比巨大的。事实上,换一个角度,把问题稍微转换一下,这道题立即迎刃而解。
我们假设至少需要n次通电,必然可以找出x灯泡。
把i号开关的状态看做一个无重复元素的集合AiAi,其元素代表着i号开关打开过的通电轮次数,对于任意的整数a∈Aia\in Ai,必有1≤a≤n1\leq a\leq n。
例如2号开关A2={1,4,6}A2=\left\{ 1,4,6 \right\},意味着在第1、4、6次通电时,2号开关是打开的。其余通电时是关闭的。
为什么要这么做?因为我们要找出故障灯泡只能通过2个特征来判断:
1.没有打开x号开关,x号灯泡却亮了。
2.打开了x号开关,x号灯泡却没亮。
那么,一旦某个开关打开的通电轮次恰好与另外若干个开关的轮次完全重合,即存在Ax=Ai∪Aj∪...Ax=Ai\cup Aj\cup...,我们将无法判断灯泡x的亮灭,究竟是由开关x控制的,还是由开关i+开关j+...控制的。例如以下情况:
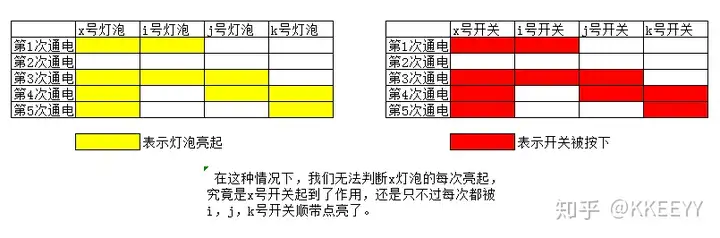
因此,如果把全集A(如果没有出现任何故障特征即可判断为全集对应的开关)与空集考虑进去,这个问题就转化为了一个集合问题:
对n个不同元素组成的集合A,定义其子集族P,使得对于P中任何一个元素Pi,P中存在的Pi的全部真子集的并集不等于Pi。已知P最多包含13个元素,求n的最小值。
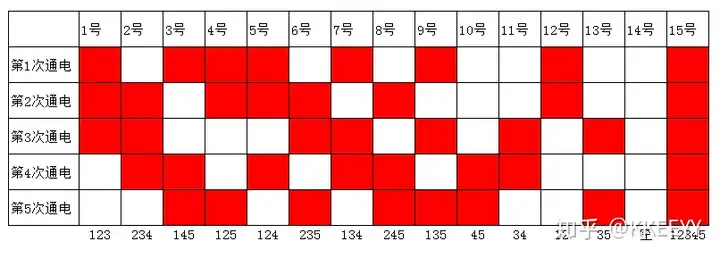
接下来的工作就是枚举了,其实寻找这13个子集并不是一件容易的事情,而且似乎并没有一种有效的方法可以直接生成满足条件的子集族。由于C(5,3)是最大二项系数,且每种组合都可以是多个C(5,2)组合的并集,因此我枚举时的直觉想法是将C(5,3)的组合尽可能多的塞进去,剩下的再用C(5,2)来补充。经过尝试,我们会发现当n=5时,恰好能找到13个这样的真子集。加入全集与空集后即可得到最终答案。下图给出了其中一种可行的方案:
四.五人博弈

去年有一位脑洞特别大的伙伴曾说起了一个关于5个人和5个山洞的故事。就在大家还在讨论这个5个人中有多少男孩子和女孩子的时候,我说要不让他们玩一个游戏吧。事实上,这并不是一个十分严谨的题目。这个问题的娱乐性是要强于逻辑性的,相比一道智力题,这个问题似乎更适合做为一个故事或是游戏。过多的分析就不说了,仅提供一个思考方向(或者说编剧方向?)。
3号是决定一切的关键。如果1号和2号进入了同一个山洞,3号也进入必然可以导致5人全灭。如果3号不进入1,2号的洞穴,则3只能通过贿赂让4,5号进自己这边,然而,3号能提供的贿赂资金一定是少于1号加2号的,明白这一点的3号知道自己横竖是死,一定会去拉1,2号垫背。
因此,3号要做的,就是告知1,2号,自己是清楚这一点的!直接告诉1号和2号:你们分开,2人还可以公平竞争,各有50%的概率存活,但一旦你们2人合作,那我必然只能拉你们垫背,自己考虑哪种情况存活的概率更高!
在拿到1,2号的贿赂资金后,3号再去买通4号就行了。因此,最终存活率最高的人是3,4,5号。
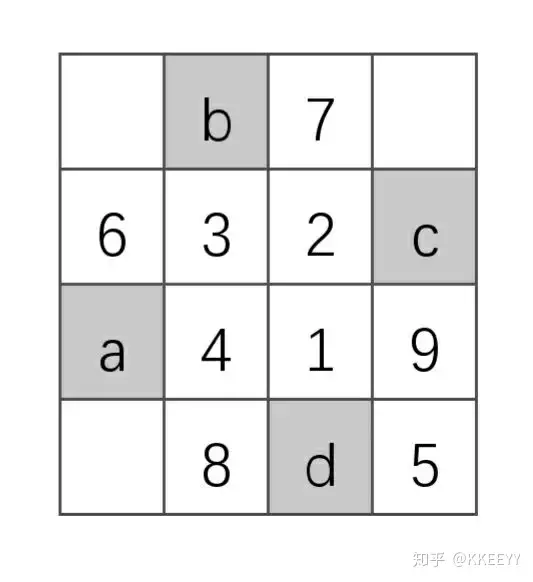
五.人与桩
这是一个典型的被我遗忘的问题。我已经完全想不起来为什么我会把它定为1星难度,至少我现在尝试重新解决它时,并没有觉得非常容易....
很显然,这个问题的解肯定不止一个。考虑到6+7+7+8=28,而木桩只有9个,这意味着每个木桩都要被平均3个人看到,这个数量是非常多的。因此,我们不妨先确定好人位置,寻找另外3个能够尽可能多存在视线重合点的位置,然后再去编排木桩。稍加尝试应该就能得到答案。这里只提供一种可行的解法作为参考,其余答案可自行验算。
六.囚犯游戏(二)

这是一个经过精心设计的,比较具有挑战性的问题。事实上,确保9名囚犯全部获得释放的策略是存在的。
约定按照提问顺序将9人编为1到9号,第一个提问的人为1号。那么:
1号囚犯只能提问,没有机会回答,因此无法向其他人传递任何信息。
2号囚犯会被1号询问1次,在这次询问中,2号可以通过回答是或否来传递2种不同的信息。
3号囚犯会被1、2号各问1次,他可以选择在1号询问时回答是,或者在2号询问时回答是,或者全都回答否,因此3号可以传递3种不同的信息。
以此类推,9号囚犯可以传递9种不同的信息。
囚犯们可以一开始约定,把所有的信息对应成为数字。那么2号囚犯可以利用回答询问的形式,告诉所有人0到1之中的一个数字。3号囚犯则是0到2,...,9号0到8。
以上是解答本问题最基础的共识。
首先解释一个原理。对于任意的n个正整数a1,a2,...,ana1,a2,...,an,以及正整数k,令S=a1+a2+...+anS=a1+a2+...+an,如果已知其中n-1个整数的值,以及SS除以k的余数,我们必然可以求出未知整数(假设为aiai)除以k的余数。若ai<kai
简要证明:假设还存在另一个整数ajaj与aiai同余,那么必然有|ai−aj||ai-aj|整除k,但由于ai,aj<kai,aj
嵌入本题情景的话,i号囚犯可以看到其余所有囚犯的数字并求和,然后将和除以i的余数告知所有人。其余的每一名囚犯,则可以结合除i号囚犯以外的其他7名囚犯的数字,知道自己头顶数字除以i的余数是多少。
然后再解释另一个概念:非等位进制,指的是一个数的每一位的进制都是不一定相同的。其实这种进制在生活中很常见,例如年月日,时分秒。
囚犯们需要用到的进制方式为8765432进制,即第一位是2进制,逢2进1。第二位是3进制,逢3进1,以此类推。例如,在此进制下的运算时这样的:
0004321+0000001=0010000;
为什么要用这种进制?因为9名囚犯能传递的数字的范围(最大值)刚好分别为2到9。同时注意到2*3*4*5*6*7*8=40320,刚好可以覆盖40000这个数。
囚犯们需要将0到40000的每个数转化成这种进制的形式,然后将每个位上的数字单独拿出来看。每一个位数安排一个囚犯通过对其他所有囚犯的该位数上的数字求和后求余,并告知其他囚犯,例如,i号囚犯将其他所有囚犯数字的第i-1位求和,再将和除以i的余数告知他们,由于i-1位的数字必然小于i,因此除了i号囚犯以外,其余囚犯均可知道自己数字的第i-1位的值。
但是,此时除了1号和9号囚犯,其余所有囚犯都只是让别人知道了某一位的数字,却不知道自己通报的对应位数的数字。因此最后再安排9号囚犯,将2号囚犯数字的第1位,3号囚犯数字的第2位,...,8号囚犯数字的第7位,同样求和后将除以9的余数告知。
这样一来,所有囚犯就全都知道了自己的数字。
七.恶魔测试

虽然只问了需要挑选多少位同学参加考试,但是,如果不能给出每位同学具体的答题方案,而仅仅只给出参加考试的同学数,那么这个答案也是得不到支撑的。事实上,满足条件的方案是存在的,并且可以很容易的构造出来。
为了表述方便,我们约定:每一个4位的3进制数都称为一种答案,其每一位上的数字都恰好对应一道题的选项。对于答案a与答案b,定义运算a◎b,其结果等于a与b各个数位上的数字相同的位数,例如:1230◎0231=2。如果a◎b≥3,则称a覆盖b。将可以被a覆盖的所有答案组成的集合(包含a本身)用La来表示。
先计算需要参考的理论人数。所有可能的答案种数只有3×3×3×3=81种,而对于其中任意一种答案a,La必然恰好包含C(4,3)×C(2,1)+1=9个不同答案。因此,理论上我们至少需要81/9=9个答案才能刚好覆盖全部的答案。
由于每种答案能覆盖的答案数恰好都是9种,因此,如果使用多于9个答案去覆盖全部81种情况,会导致必然存在某些答案,被不止1个答案覆盖,即存在用于覆盖的答案a与b,使得La∩Lb≠∅。而题目对于及格人数的要求是"恰好存在",因此,当要求恰好1人及格时,用于覆盖全体答案的答案个数只能"恰好"是9个,每个答案对应给一个人。而题中要求的恰好2人,其实只需要将9个答案再重复一次,用一共18个答案就可以了。因此,潘多拉挑选的人数,只能是18人。
到目前为止,我们虽然能够知道一定只能是18人,但潘多拉具体跟每一位同学交代了什么呢?满足条件的9个答案真的存在吗?如果直接去枚举这9个答案并验证,这个工作量是非常大的。有一位迷题爱好者曾告诉我,他尝试过通过家用电脑写程序来枚举,计算机运行了1个多小时的时间才得到第一组解。实际上,满足条件的解是很容易通过人脑构造出来的。
对于答案a与b,显然当且仅当a◎b≤1时,有La∩Lb=∅,这一点通过列举出具体例子就可以很直观的看出来。因此我们可以将原问题转换成:寻找答案个数为9的集合X={a1,a2,...,a9},使得对于任意不同的i,j≤9有ai◎aj≤1。
下图中,每一列代表一道题,每一行代表一个选项。编号1到9分别代表9个人的答案。我们不妨设第123个答案的第一位选项数字是相同的。那么,123的后3位数字必然互不相同。
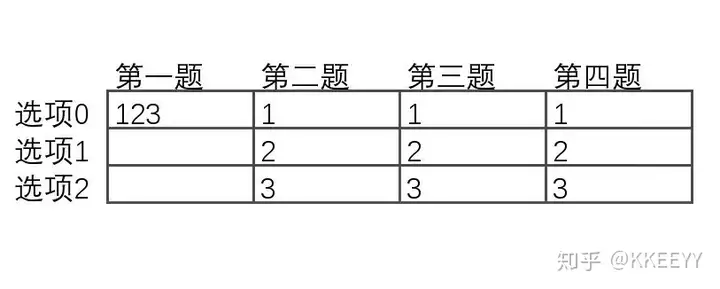
现在再加入456,但是在加入第二、三、四题时需要注意,除了456本身需要错开,还要确保与123分别错开,只需要每次向下位移一个选项就可以做到。
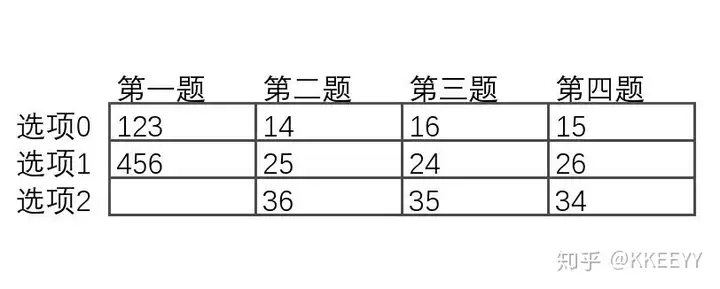
同理再加入789,这次则每次向下位移2个选项。
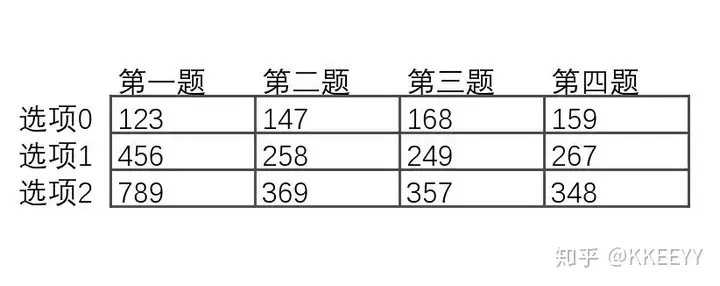
这样便得到了一种可行的方案,而它本质上其实就是一个经典的"柯克曼三元系"。
八.投票困境

这是一个有趣的问题。从发布至今我已经看到过很多个有意思的解法。我认为,任何发散性的解法只要不违背题设中的基本规则,都是可行的。
我自己的解法是这样的:选择一位最可靠的少年作为计票员,在心里随便想一个8位的数组,比如【2,0,11,8,7,2,6,5】,然后将这个数组以悄悄话的方式告诉下一位少年。8个数字分别代表8个少年,第二位少年想投哪个少年,就在对应的数字上加1。比如他想2号2票,5号1票,那么他将数组【2,2,11,8,8,2,6,5】再悄悄告诉第三个少年就行了。这样一直到最后一位少年,再将数组悄悄告诉计票员,计票员再加上自己的投票后,与最初的数组进行对比,仅公开两者之差,就是最终的投票结果。
九、排名问题

这个题现在看来好像出错了.....菊花知道无名或无名知道菊花的方法是存在的,但是让双方都知道的办法我怎么也想不起来了......等以后想起来了或是能够证明符合要求的方法不可能存在之后再来更改吧...
十、双胞胎实验

目前我不知道这个问题最终答案是什么。最好的答案目前是4枚硬币。以下是来自贴吧-智力题吧用户gf10025的解答:
4枚硬币。在关入房间前,将房间和双胞胎分别编号1到16,那么在关入房间后,有
房间号=人编号+x……①
房间号=人编号+x-16……②(0≤x≤15)。
当任意一个人编号和房间号的x都不相同时,②肯定存在(16和15不可能同时在对应的16或15房间),有
房间号总和=人编号总和+(0+1+2+……+15)-16k
房间号总和与人编号总和相等,有
8*15=16k
k无整数解。既①和②必然有至少两人的x相同。记相同的x的值为a,所有人都在自己编号上增加a,就至少有两人符合要求。而a的值在0到15,所以4枚硬币就足够表示出a的值
十一、抓捕逃犯
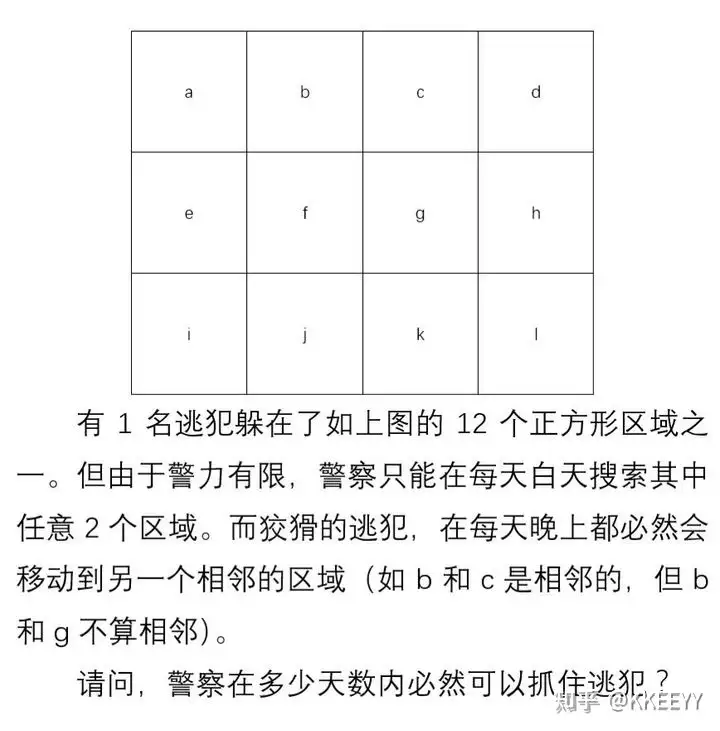
最早是在潘多拉那里看到过这个问题,不过原题中仅需要给出3个可搜素区域的方案。后来我有天闲着无聊时又翻到了这个问题,在稍加发散的思考后,惊讶的发现其实2个可搜索区域也是能够做到的。以下是来自知乎用户raoxj的解答:
容易发现这个题等价于下面这个单人游戏:有一个3*4的12格棋盘,一开始都是白色。每次可以选择两格染黑,然后之后所有有相邻白格的格子都变成白色;否则变成黑色。目标是把所有格子染黑。
显然开局除了选be(或者对称的四组格子)之外的任何两格都是毫无意义的(染黑后直接又全都变成了白色)。于是第一步只能选be,状态变为a黑其它都白。注意到下一步之后a一定会变白(因为再选be等于没有任何变化),所以只能选fi配合a包围e(或者选cf包围b,但是后面一样);之后b变为黑色其它全白。这时只能选bj正好围住ai;之后ai黑其它全白。然后也只能选cf(或者对称的kf)配合ai围住be…这时候规律已经很明显了;在8步之后可以把棋盘染成黑白间隔的状态。比如如果按上面描述的方法(be/fi/bj/cf/gj/ck/dg/hk)现在棋盘状态是1010/0101/1010(1为白)。
这时即使什么也不做棋盘也不会再增加任何白格了,但是还需要点掉剩下的六个白格。显然除了涂黑hk(或者对称的ch)外其它操作都没有任何作用;之后每步都只有一个选择(除去对称的情况),并且正好是前面8步反过来。于是最少需要16天:be/fi/bj/cf/gj/ck/dg/hk/hk/dg/ck/gj/cf/bj/fi/be。
注意到这个思路可以推广到任意3*n的情况,同时可以发现如果棋盘长宽都不小于4则无解。
十二、可能的谜题

这个有趣的逻辑谜题存在着各种各样不同的版本,不过基本上最终的结果都是参与问答的人都知道了。有一天在思考这个问题时突然觉得我是不是可以更改一下剧情呢?于是有了本题。
这个问题最简单的解法就是暴力排除,因为总共只有以下12种情况,排除起来并不麻烦:
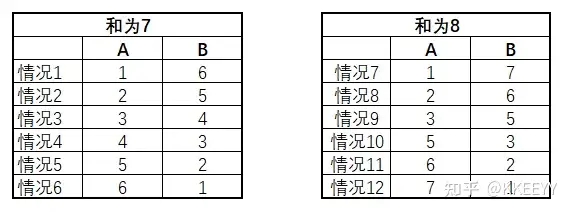
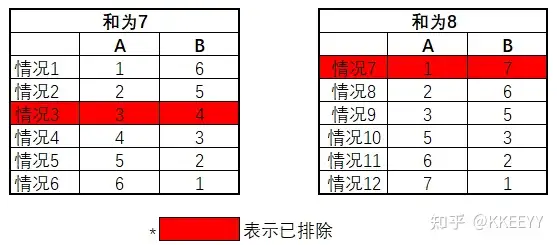
接下来一句一句分析。根据第一句话:A说我不知道,可以排除情况3、情况7。因为这两种情况中B的数字所对应的A自己的数字是唯一的,如果A看到B为4或7,则可以判断出自己的数字只能为3或1。如下图:
根据第二句话:B说我不知道,从剩下的情况中,同理可以排除情况1、情况4、情况9、情况12。因为这4种情况下A的数字所对应的B的数字都是唯一的。结果如下:
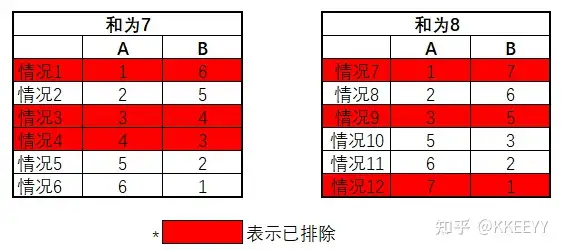
根据第三句话:A说我知道了,说明此时A所看到的B的数字对应的情况是唯一的,因此排除情况5、情况11。否则,如果A看到B为2,则将无法判断自己究竟是5还是6。结果如下:
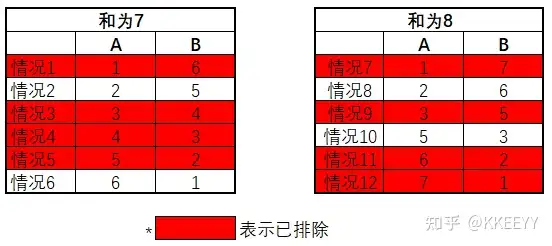
根据第四句话:B说我不知道,说明此时B看到的A的数字所对应的情况中自己的数字并不唯一,因此排除情况6、情况10。最终,只剩下情况2和情况8,而在这两种情况中,A的数字都为2。最终结果如下:
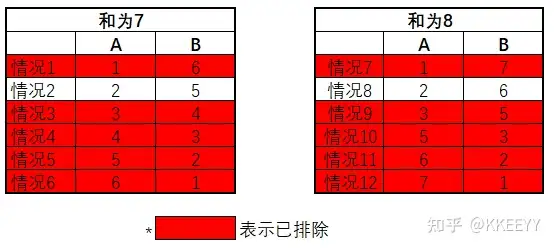
十三、困局合作

首先从严格意义上来说,目前本题是暂时没有找到最终答案的,因为证明某个方案或天数是最少似乎是一件非常困难的事情,并且我个人认为意义不大。我认为这个问题真正的乐趣在于不断优化方案的这个过程,通过各种方法与技巧将天数不断缩减。目前我所知的最优的答案为199天,不过其正确性还有待验证。相比之下201天是一个比较容易想到的结果,以下是来自百度贴吧——智力题吧用户东山老僧201天的方案:
201天的一种方法:
首先把所有人编号0-99。
第一阶段:101天
策略:
拿到正面的人:写自己的编号,当收到通知后,写无穷大。
拿到反面的人:写自己的编号+100。当收到第一次通知后,写自己的编号+200。当收到第二次通知后,写负无穷。
第一阶段结束后,仅有拿到反面的编号最小的人将收到两次通知(其他人均只收到一次通知)。此人已经得知正面的人数和反面的人数,可以称之为智者。当然如果所有人都是正面,就没有智者。
第二阶段:100天
策略:
除智者外的所有人:策略与第一阶段相同。
智者:
如果正面多于反面:每天都写无穷大。
如果正面反面相等:每天都写负无穷。
如果正面少于反面:第一天写负无穷,此后每天都写无穷大。
第三阶段:猜测
策略:
除智者外的所有人:
如果自己在第二阶段没有收到通知:猜一样多
如果自己在第二阶段收到通知的天数与第一阶段相同:猜{自己拿到的那一面}比较多
如果自己在第二阶段收到通知的天数与第一阶段不同:猜{自己没拿到的那一面}比较多
智者:略。
以上是201天的方案。以下是来自qq用户千恋万花199天的方案(暂未严格验证其正确性,大概看起来是正确的,先提供在这里作为参考,以后有空的时候再来检查):